Chaos is the science of process rather than state. Of becoming rather than being. Now that Science is looking, chaos seems to be everywhere. A rising column of cigarette smoke breaks into wild swirls. A flag snaps back and forth in the wind. A dripping faucet goes from a steady pattern to a random one... (Gleick 1987)

         As long as I can remember, I’ve been fascinated by the sound of a dripping faucet. Its steady beat with unanticipated syncopations can be mesmerizing. When the drops fall into a small pool of water this natural process occasionally produces a very interesting melody. Experimental music composers and scientists share a similar process of discovery. When Inspiration Came takes its name from a line in James Gleick’s book Chaos: The Making of a Science. Gleick provides a compelling account of how scientists like Mitchell Feigenbaum and Robert Stetson Shaw used computers to explore the boundary between order and chaos in the 1970s. Feigenbaum’s study of the logistic equation, (Gleick 1987, pp. 166-80) a simple chaotic model for population growth, and Shaw’s experiments with a dripping faucet (Gleick 1987, pp. 262-67) led to important discoveries in chaos theory. The work is a sonic journey through the logistic equation, or more specifically, the logistic map.

         My first encounter with the logistic equation was via Scientific American's Computer Recreations column (Dewdney 1987). In about 1845, Belgian mathematician Pierre Verhulst formulated it as a model of population growth and is commonly written today as (Weisstein 2009d):

(1)

The variable x may assume real values from 0.0 to 1.0 and is calculated by successive iterations of the equation. The variable r, sometimes called the growth factor, drives the process and may range from 0.0 to 4.0. When the value of r is between 0 and 1 the value of x remains 0. When the value of r is between 1 and 3, however, the value of x grows in a steady fashion. As the value of r slowly approaches 3.56–a value often referred to as the strange attractor of the equation–the values begin to bifurcate or split in two, alternating between 2 values, then 4, then 8, etc. Then, almost magically near the strange attractor, the values become essentially random. This progression is shown in Fig. 1.  

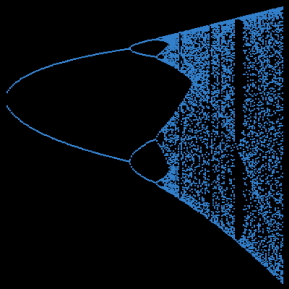
Fig. 1. A graph of the logistic equation.

         As composer Gerald Bennett and many others have noted, deterministic chaotic processes such as these may be used to create self-similar musical structures (Bennett 2009). This composition is a sonic journey through the logistic equation whose macrostructure is determined by the golden ratio (Devlin 1994).

(2)

The work's microstructure, however, is determined by equation (1) using granular synthesis techniques that make it possible to turn a single drip into a rainstorm and back again. After a brief introduction, the work presents 254 iteration of equation (1). Each iteration occupies one beat, whose duration is defined by the steady drips near the outset of the work. The a section spans exactly 157 beats, whereas the b section spans 97 beats. Throughout the work, I strategically reset the value of r to generate interesting drip melodies and control the granular variations. The work's microstructure, at times, mirrors the bifurcations and labyrinthine complexities of the logistic equation. Beneath the granular surface, a supporting chorus of four pink noise ostinati "sing" randomly-selected harmonic partials of fundamental pitches whose relations are derived from a Logistic-map inspired splitting of the octave into two equal parts. The final element of the composition is a solo performer who, using a Wiimote game controller (Nintendo 2009), controls the pitch, timbre, and spatial orientation of a fifth pink-noise instrument in an ongoing dialogue designed to reinforces the evolutionary trends of the computer-generated musical surface.

         This work is dedicated to my former teacher and collaborator, choreographer Lynne Anne Blom, who suggested I use James Gleick's book as a source of artistic inspiration.

References

Bennett, Gerald, 2009. Chaos, Self-Similarity, Musical Phrase and Form.
     http://www.gdbennett.net/texts/Chaos.pdf.
Dewdney, A.K., 1987. "Computer Recreations: Probing the Strange Attractions of Chaos,"
      Scientific American (July), p. 108.
Devlin, Keith, 1994. Mathematics: The Science of Patterns.
      New York: Scientific American Library, pp. 108-09.
Gleick, James, 1987. Chaos: Making a New Science. New York: Viking, p. 5.
Nintendo, 2009. Wiimote is a nickname for Wii Remote, TM, ® and © Nintendo.
     http://wii.com/http://wii.com/.
Weisstein Eric W., 2009a. "Bifurcation," from MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/Bifurcation.html.
______________, 2009b. "Golden Ratio," from MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/GoldenRatio.html.
______________, 2009c. "Logistic Equation," from MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/LogisticEquation.html.
______________, 2009d. "Logistic Map," from MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/LogisticMap.html.
______________, 2009e. "Strange Attractor," from MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/StrangeAttractor.html.
______________, 2009f. "Self-Similarity," from MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/Self-Similarity.html.

Updated: January 12, 2012