Conceived for and executed in the digital audio signal processing environment Csound, Strange Attractors & Logarithmic Spirals sets into opposition sonic manifestations of two beautiful mathematical forms: strange attractors, chaotic systems that cycle periodically yet never repeat exactly the same pattern; and the logarithmic spiral, a familiar shape found throughout nature in shells, tusks, sunflowers, galaxies and so forth.

     The work features two contrasting approaches to synthesis: one inspired by an instrument design by Csound guru Hans Mikelson, the other by music-scientist Jean Claude Risset. The Mikelson instrument is a sonification of the Lorenz attractor (Boulanger 2000), the chaotic system of three differential equations discovered by scientist Edward Lorenz shown below (Lorenz 1993).

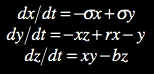(1)

When initialized with a special set of values, the values used in this composition, a graph of system (1) produces a beautiful butterfly-shaped pattern.

The sound quality of the Lorenz attractor instrument varies from noise-like pulses to percussive zips and buzzes. The Risset instrument (Gather 2009), on the other hand, generates sounds of an entirely different nature. Risset's ingenious additive synthesis technique produces a cascading arpeggio in the harmonic series, a technique that offers precise control over the arpeggio's pitch content and rate of speed. The sustained sounds produced by the instrument range from organ-like sounds to the sounds produced by a Tuvan throat singer.

     All of the musical parameters of this composition are derived, in one way or another, from the Fibonacci sequence (Kramer 1973),

1, 1, 2, 3, 5, 8, 13, 21, ...,

and its connection to the golden spiral (Weisstein 2009c),

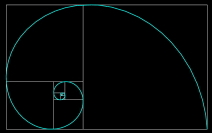
and the golden ratio (Livio 2002).

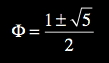
The divine proportion has a long and distinguished history as a source of inspiration for artists (Hemenway (2005). It is expressed in the structure of the music in myriad ways including as the pitch interval (1.618:1) spanned by many of the glissandi and as the key to which the work modulates.

The work is dedicated to my undergraduate research mentor Kenneth Grant who encouraged me to explore the boundaries of science and music using computers.

RB

references

Boulanger, Richard ed., 2000. The Csound Book. Cambridge, MA: MIT Press, pp. 379-80.
Gather, John-Phillip Gather, ed., Amsterdam Catalogue of Csound Computer Instruments (ACCCI),
        Instrument 02_43_1. http://www.music.buffalo.edu/hiller/accci/
Hemenway, Priya, 2005. Divine Proportion. Phi: In Art, Nature, and Science.
        New York: Sterling Publishing Co., 2005, pp. 90-114.
Kramer, Jonathan , 1973. "The Fibonacci Series in Twentieth-Century Music."
        Journal of Music Theory, Vol. 17, pp. 110-48.
Livio, Mario, 2002. The Golden Ratio. New York: Broadway Books.
Lorenz, Edward, 1993. The Essence of Chaos. Seattle: Washington University Press, pp. 188-89.
Weisstein, Eric W, 2009a. "Fibonacci Number," from MathWorld--A Wolfram Web Resource.        
        http://mathworld.wolfram.com/FibonacciNumber.html
______________, 2009b. "Golden Ratio," from MathWorld--A Wolfram Web Resource.
        http://mathworld.wolfram.com/GoldenRatio.html
______________, 2009c. "Golden Spiral," from MathWorld--A Wolfram Web Resource.
        http://mathworld.wolfram.com/GoldenSpiral.html
______________, 2009d. "Logarithmic Spiral," from MathWorld--A Wolfram Web Resource.
        http://mathworld.wolfram.com/LogarithmicSpiral.html
______________, 2009e. "Strange Attractor," from MathWorld--A Wolfram Web Resource.
        http://mathworld.wolfram.com/StrangeAttractor.html