A live-interactive composition for laptop computer, The Music of the Primes is a musical exploration of the spacing of prime numbers, numbers that cannot be expressed as the product of two smaller numbers. Fig. 1 shows the first 100 counting numbers with primes indicated in bold type.

Fig. 1. The first 25 prime numbers.

In his book of the same title, mathematician Marcus du Sautoy describes the primes as the "atoms of arithmetic," the "mathematician’s periodic table," the "irregular heartbeat of mathematics," and even more prosaically, as "jewels studded in the infinite universe of numbers." Fig. 2 reveals that irregular heartbeat.  

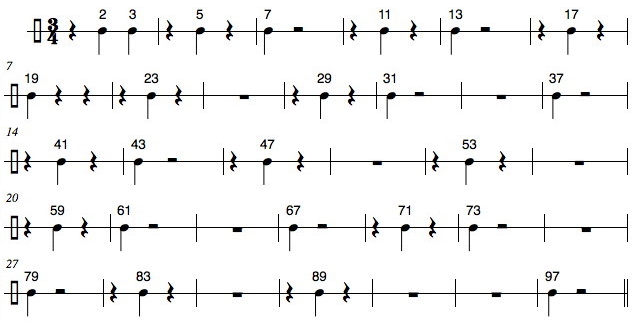Fig. 2. A rhythm created from the spacing of the first 25 primes.

Arbitrarily notated in triple meter, Fig. 2 is but one of many possible sonifications of Fig. 1 (Burke, et al. 2005).

     One of the basic “laws” of perception, figure and ground refers to our ability to perceive separate visual elements based on contrast. Figure/ground reversals often create wonderful paradoxes. For example, note the “confusion” that results from the following black and white image.

Fig. 3. A paradoxical figure/ground reversal in the visual domain.

Similar types of reversals may be constructed in the musical domain. For example, returning to the rhythm in Fig. 2, the primes could serve as the figure–i.e., a series of prime-inspired accents–against the ground implied by the steady beat of counting number continuum. This musico-mathematical idea is shown in Fig. 4 for the first 33 counting numbers.

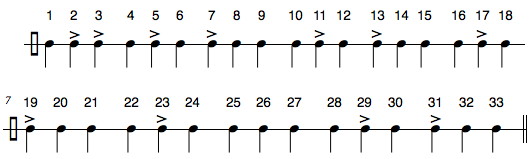
Fig. 4. A prime-inspired figure/ground reversal in the musical domain.

     Notice that the primes seem to “thin out,” or get more widely spaced, as the numbers get larger (see Fig. 1). Experimentation with the rhythms shown in Fig. 2 and Fig. 4 did not yield interesting musical results, so I tried repeated prime cycles, an approach inspired by the ancient Greek mathematician Eratosthenes’ sieve method for identifying primes. The first four prime cycles are shown in Fig. 5.

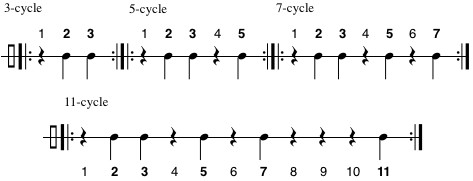
Fig. 5. Prime Cycles (against background pulse).
3- 5- 7- 11-

The algorithmically-generated percussion part is created by layering prime cycles of increasing magnitude. The prime cycles are assigned to different percussion instruments so they may easily be heard. For example, in the introduction to the work: a bass drum presents the 3-cycle; then a shaker, entering at beat 37, adds the 5-cycle; at beat 83 a conga enters, adding the 7-cycle; at beat 113, a rim shot enters adding the 11-cycle; at beats 127, 131, and 137, respectively, a triangle, tambourine, and high-low congas add the 13-cycle, 17-cycle, and 19-cycle. Notice how the staggared entries mimic the spacing of the primes, and how the accumulation of seven stratified layers of prime cycles creates a dense polyrhythmic texture I call a prime-cycle sieve. The sieves corresponding to the first three sections of the work are shown in Fig. 6.

3, 5, 7, 11, 13, 17, 19
5, 7, 11, 13, 17, 19, 23
7, 11, 13, 17, 19, 23, 29
etc.
Fig. 6. Prime-cycle sieves.

Higher order sieves are explored until the climax of the work when the patterns begin to slowly shift their way back to toward the opening configuration.

     The pitch domain is also saturated with various manifestations of prime spacing. For example, Fig. 7 shows the just (29-limit) prime tuning created specifically for this work.

Fig. 7. The just (29-limit) tuning created for The Music of the Primes.

Notice how this tuning is derived from the spacing of the first 10 primes. The proportions in Fig. 7 indicate relative frequency ratios with respect to Eb. Fig. 8 shows the same frequency ratios arranged in ascending semitones to create a chromatic scale on Eb4.

Fig. 8. A chromatic scale derived from the spacing of the first 10 primes.

     Fig. 9 shows the main theme of the Music of the Primes, a theme which makes its first appearance about 55 seconds into the work.

 

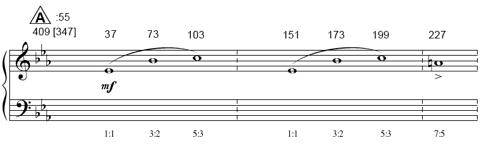
Fig. 9. A theme created from the prime-inspired interval ratios 3:2, 5:3, and 7:5.

Notice how this theme explores the spacing of the primes in various ways. For example, its pitch intervals (3:2, 5:3, and 7:5) are derived from the spacing of the primes. Furthermore, the score makes use of an unconventional prime-inspired proportional notation. Pitch events are noted in sequential order using whole notes (not to scale), and the start time of each pitch event is given above the staff using absolute pulses with respect to the beginning of each section. For example, section A begins 55 seconds into the work at pulse 409. With respect to rehearsal letter A, the first note of the main theme begins on pulse 37, the second note on pulse 73, the third note on pulse 103, and so on. Of course, these are just a few examples of the prime-inspired pitch and rhythmic structures that may be found in the work.

     The Greek mathematician Euclid proved that there are infinitely many primes. In many ways, this work is an attempt to make the infinite finite and musically engaging. It is an homage to Euclid and Eratosthenes, as well as Gauss, Riemann, and other mathematicians who have contributed to our appreciation of the beauty, mystery, and music of the primes.

RB

references

Burk, Phil, Larry Polansky, Douglas Repetto, Mary Roberts and Dan Rockmore, 2005.
     “Sonification,” in Music and Computers: A Theoretical and Historical Approach.
     Emeryville, CA: Key College Publishing.
     http://digitalmusics.dartmouth.edu/~book/MATCpages/chap.1/1.pops/1.1.sonif.html
du Sautoy, Marcus (2003). The Music of the Primes. New York: Harper Collins. See also,
     http://www.musicoftheprimes.com
Weisstein, Eric W. "Prime Number." From MathWorld--A Wolfram Web Resource.
     http://mathworld.wolfram.com/PrimeNumber.html